

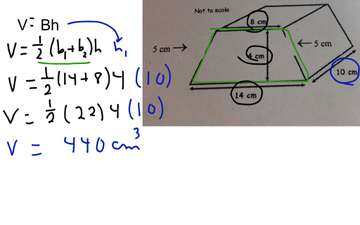
The perimeter of the trapezoid is 'P', and 'H' is the height of the prism. In this formula, 'b1' and 'b2' stand for the length of the bases of the trapezoid. Descriptive geometry with stereoscopic figures. The surface area of a trapezoidal prism can be given with this formula: (b1+b2)h + PH. The study of figures and geometric bodies: activities for the first years of schooling. One of the most common objects that have the shape of a trapezoidal prism is a gold ingot or ramps used in motorcycle racing. Since the volume of a prism is defined as V = (area of the polygon) x (height), we can conclude that the volume of a trapezoidal prism is V = Txh. Therefore, the area of the surface of a trapezoidal prism is A = 2T + P1 + P2 + P3 + P4. The area of a trapezoid is defined as T = (b1 + b2) xa / 2 and the areas of the parallelograms are P1 = hxb1, P2 = hxb2, P3 = hxd1 and P4 = hxd2, where"b1"and"b2"are the bases of the trapezoid,"d1"and"d2"the non-parallel sides,"a"is the height of the trapezoid and"h"the height of the prism. The two legs of the trapezoid are labeled 10 cm. The larger base is labeled 15 cm and the shorter base is labeled 5 cm. To calculate the surface area of a trapezoidal prism, we need to know the area of the trapezoid and the area of each parallelogram involved.Īs seen in the previous image the area involves two trapezes and four different parallelograms. Explanation: Given: a trapezoidal prism The base of a prism is always the trapezoid for a trapezoidal prism. The height of the trapezoid base is labeled 7 cm. Trapeze scalene : is that trapezoid that is not isosceles nor rectangle its four sides have different lengths.Īs you can see according to the type of trapezoid used will obtain a different prism. Tracecium isosceles : is a trapezoid such that its non-parallel sides have the same length. A right prism is a solid (or 3D) object with two parallel bases or ends that are identical and flat faces that are rectangles.
Rectangle trapezoid : it is that trapezoid such that one of its sides is perpendicular to its parallel sides or that it simply has a right angle. In the particular case of the trapezoid we can find three different types of bases: You can also have an oblique trapezoidal prism, whose construction is similar to the previous one, you only have to draw the four lines parallel to each other.Īs said before, the shape of the prism depends on the polygon. Then, from each vertex, a vertical line of length"h"is projected and finally another trapezo is drawn so that its vertices coincide with the ends of the lines drawn previously. To draw the straight trapezoid prism you begin by drawing a trapezoid. To draw it, it is first necessary to define what a trapezoid is.Ī trapezoid is an irregular polygon of four sides (quadrilateral), such that it has only two parallel sides called bases and the distance between its bases is called the height.
#Right trapezoidal prism how to
To see the characteristics of a trapezoidal prism, you must start by knowing how to draw, then what properties the base meets, what the surface area is, and finally how its volume is calculated. (a) Leo is asked to purchase roping that will be used to close off the area around the statue. As Leo paints the stand, he calculates the surface area of the stand to be 35 ft2. The base of the prism has an area of 3 ft2, and the prism stands 3.2 feet high. Therefore, it depends on which quadrilateral is involved. The stand is in the shape of a right trapezoidal prism. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.81' for the name truncated prism, but I cannot find this book.If the polygons involved in a prism are squares, then this is different from a prism involving diamonds for example, even though both polygons have the same number of sides. (I integrated the area of the horizontal cross-sections after passing the first intersection with the hyperplane at height $h_1$ these cross-sections have the form of the base triangle minus a quadratically increasing triangle, then after crossing the first intersection at height $h_2$ they have the form of a quadratically shrinking triangle)ĭo you know of an elegant proof of the volume formula? I was also able to prove this formula myself, but with a really nasty proof.

(where $A$ is the area of the triangle base) online, but without proof. I needed to find the volume of what Wikipedia calls a truncated prism, which is a prism (with triangle base) that is intersected with a halfspace such that the boundary of the halfspace intersects the three vertical edges of the prism at heights $h_1, h_2, h_3$.


 0 kommentar(er)
0 kommentar(er)
